

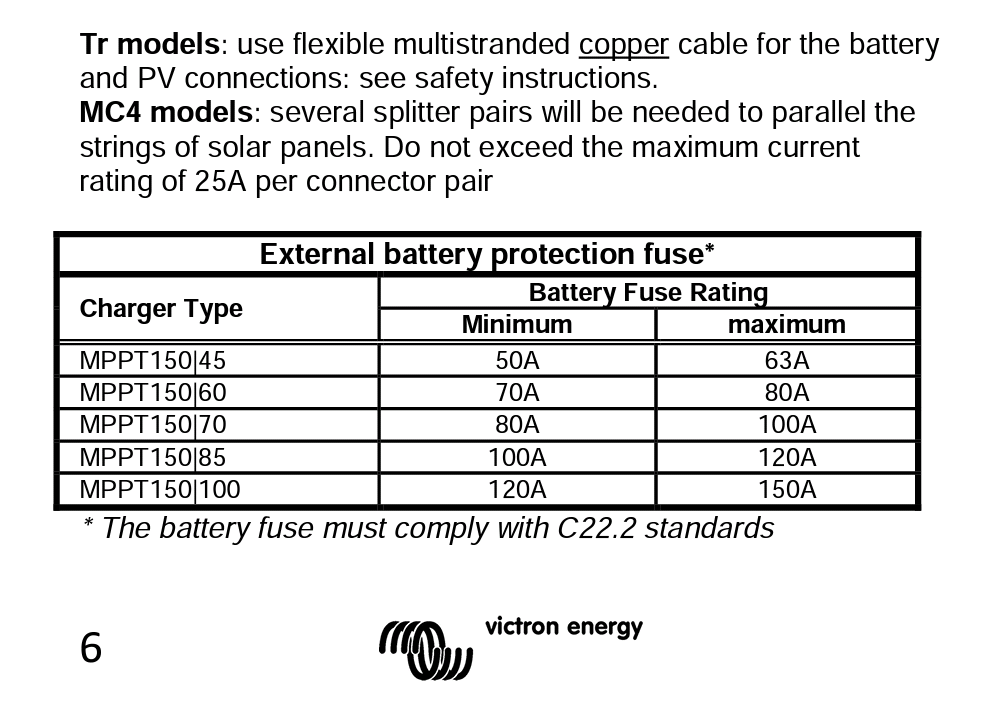
12vdc wire size chart how to#
Then, refer to the table below to find the minimum wire gauge for this cross-sectional area.ġ3 AWG How to Calculate the Maximum Conductor Length Then, multiply by 1,000,000 to convert the cross-sectional area in square meters to square millimeters. Recall that the resistivity of a copper conductor is 1.7241×10 -8 Ω Then, use our wire size calculator to find the wire gauge with the correct cross-sectional area.įor example: Find the minimum wire gauge needed for a 120V circuit drawing 20A using a 40′ long copper conductor with a max voltage drop of 3%.Ī 3% voltage drop would be 3.6 volts. You can multiply the resulting cross-sectional area by 1,000,000 to calculate the area in square millimeters. m, its length L in meters, and the current I in amps, divided by the maximum allowable voltage drop V in volts.The minimum cross-sectional area A for a conductor in square meters is equal to the product of two, the conductor resistivity ρ in Ω m) × L (m) × I (A) / V drop (V)Ī = cross-sectional area in square meters.Using the equation for voltage drop and rearranging the variables, the minimum conductor size in square meters for a circuit can be found using the following:Ī (m²) = 2 × ρ (Ω A large conductor would be a waste of money, and an undersized conductor might not be able to handle the required current flows. How to Calculate the Minimum Conductor Sizeĭepending on the application, it is important to use conductors of the proper cross-sectional area for economical and reliable power delivery. In a three-phase system, the voltage dropped V in volts is equal to the current I in amps times the square root of 3 times the conductor resistivity ρ times the conductor length L in meters, divided by the cross-sectional area of the conductor A in square meters. The formula to calculate voltage drop in three-phase systems is Voltage Drop Formula for Three-Phase Systems So, we can expect a voltage drop of 1.894 volts in this circuit. You can convert the length in feet to meters by multiplying by 0.3048. This is equal to the resistance of a conductor that is one thousand circular mils and one thousand feet in length.Ī = conductor cross-sectional area in square millimetersįor example: Calculate the voltage drop of a 120V circuit drawing 15A using a 25′ long 14AWG copper conductor.Ī 14 AWG wire has a cross-sectional area 2.081 mm² per the table below, and you can convert this to square meters by multiplying by 1,000,000. K = direct current constant – use 12.9 for copper conductors and 21.2 for aluminum conductors. V drop (V) = I (A) × 2 × K × L (m) / A mm² You may also see voltage drop calculated using an alternate formula, which calculates the conductor resistance in a slightly different way: m and the resistivity of aluminum conductors is 2.6548 × 10 -8 Ω.The resistivity of copper conductors is 1.7241 × 10 -8 Ω So, the voltage dropped V in volts is equal to the current I in amps times 2 times the conductor resistivity ρ times the conductor length L in meters, divided by the cross-sectional area of the conductor A in square meters. m)Ī = conductor cross-sectional area in square meters.Ρ = conductor resistivity in ohm-meters (Ω Thus, you can calculate voltage drop for single-phase AC and DC circuits using the following formula derived from Ohm’s Law: You can find the resistance for various conductor sizes in the chart below, or use one of the following voltage drop formulas. Ohm’s Law states that the voltage is equal to the current times the resistance. Using Ohm’s Law, the voltage can be calculated by multiplying the current by the resistance.
This current increase can overheat the circuit, causing damage to the equipment and devices. Electrical devices consume power, and when they get reduced voltages, the current flow increases to meet their power needs.
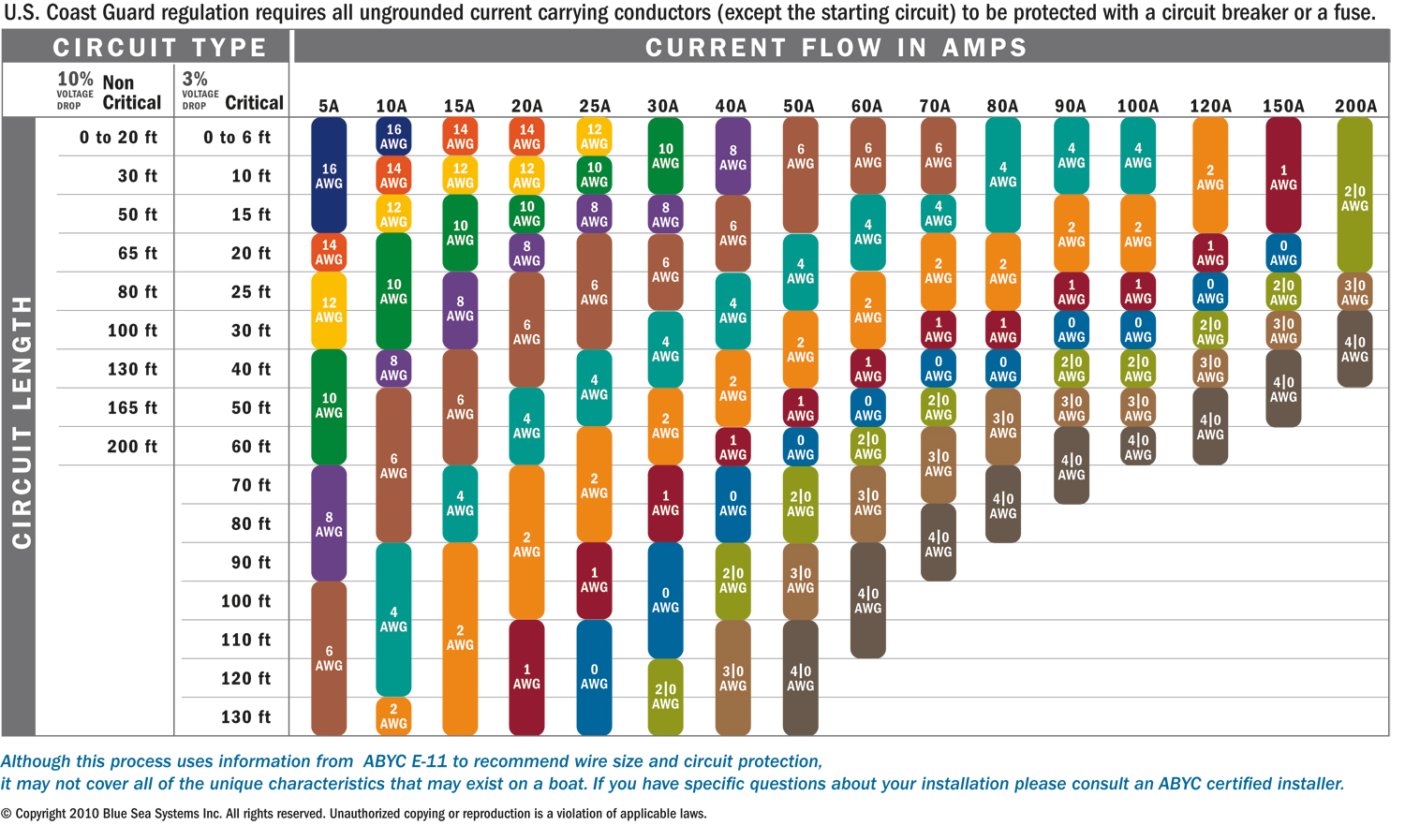
Voltage drop in a circuit means less voltage is delivered to connected devices. Voltage drop is an important consideration when planning a circuit to allow equipment using the circuit to run as designed. Voltage drop is the amount of voltage lost in a circuit due to resistance of the conductor.


 0 kommentar(er)
0 kommentar(er)
